Algorithms in CS

Jan 10, 2023Arkar Kaung Myat

CSAlgorithms

Lets take a look at what and how algorithms are use in programming.

# What is an algorithm ?

An algorithm is any well defined computational procedure that takes some values or set of values, as an input and produce some value, or set of values as an output. We use algorithms to representing solutions for a particuar set of problems in a very simple and efficient ways. If we have a definitive instruction for a set of problem we can use it in anywhere no matter what the programming language is.

Imagine we have a problem in a eCommerce application which essentially will have to add the total cost of all the selected items in the cart, how do we decide the appropriate algorithm ( an instruction ) in most efficient and simple way.

In order to design an algorithm there are some principles that we need to consider

Clear problem definition.
Constraints of the problem
An input
An output and
A solution

Clear problem definition means in this example we need to add the total prices of all the elements in our shopping cart.

The constraints of the problem, in this case, are we need to make sure the values are valid. Such as incorrect negative values or any invalid characters.

An Input which in this case can only be an array of numbers. And obviously, the output is to be expected when all the item values are added.

And a solution that should return the total values by the use of some methods which can either be by the + operator or any other possible method.
If we have all the basic prerequisites considered we are ready to write the algorithm for our shopping cart.

START
If a cart is empty return 0;
Declare total variable
Start loop from the last most item of the cart and add each item’s price to the total
return total
END

As one must follow the algorithm step by step, the instructions for the algorithm must have the following characteristics

Unambiguous, each of its steps should be clear in all aspects with only one meaning. As an algorithm is supposed to be language-independent and should be just plain instructions to be implemented easily in any language.
Well-defined input and output
Most importantly finite-ness. The algorithm must be finite and it must terminate after a finite time. Imagine you add up items in your cart and press calculate total and then the loading never stops until your computer freezes.
Last but not least an algorithm must be correct. An algorithm can be said to be correct if, for every instance of input, it halts with the correct output.

function addItems (items){
  let total = 0;
    for(let i=0;i < items.length; i++){
        total = items[i] + total
    }
    return items;
}

# What kind of problems is being solved by algorithms?

Algorithms are daily basics in the programming world and we use various types of algorithms to solve very different types of algorithms.

Even in daily life, if you are making breakfast, you follow a pancake recipe is you following the algorithm to get the perfect outcome.
Today you can find a lot of information on the internet in a quick second and the internet brings you the most suitable result for your requirement. Search engines such as google, bing uses tons of searching algorithms to help find you the best recipe for your breakfast.
Every smartphone today can recognize your face and authenticate your information using facial recognition algorithms. It takes the information from your face and compares it to the known database that is saved on your phone on your first-day setup.
Schedule systems, GPS, traffic lights and even sorting assignment papers use an algorithm to complete.

# Type of algorithms

There are many various types of algorithms and some of the most common algorithms are

Brute force algorithms
Recursive
Divide and Conquer
Backtracking algorithms
Greedy Algorithms
Dynamic programming algorithms
Hashing
Randomize algorithms and more.

# Brute force algorithms

This is the most straightforward technique while designing algorithms. In this type of algorithm before we talk about optimization we usually think to get a solution at least for us to try to optimize it later. We can solve every problem using brute force algorithms even though there might not be the best solution for time and space complexities .

function findElement(arr, target) {
  if (arr.length === 0) return false;
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === target) return i;
  }
  return false;
}

You can think of it as trying every possible combination of a safe until you unlock it.

# Recursive algorithms

Another type of algorithm is the recursive algorithm where the algorithm is based on recursive( function call itself directly or indirectly is called recursive functions). Recursive is an amazing technique that can reduce the length of our code and make it easier to read and write. In the case of algorithms, the algorithm called itself again and again until the problem is solved usually with the help of a base termination condition.

function factorial(n) {
  if (n == 0) return 1;
  return n * factorial(n - 1);
}

# Divide and Conquer Algorithms

Another popular paradigm for problem-solving is the divide and conquer algorithm. When we see a problem we divide the problem into several subproblems that are smaller instances of the same problem until they are large enough to solve them recursively. Looking back to the brute force algorithm the time complexity of the linear search algorithm may vary depending on where the element is. The later the element is the longer the iteration will take and the divide and conquer algorithm save time in this case.

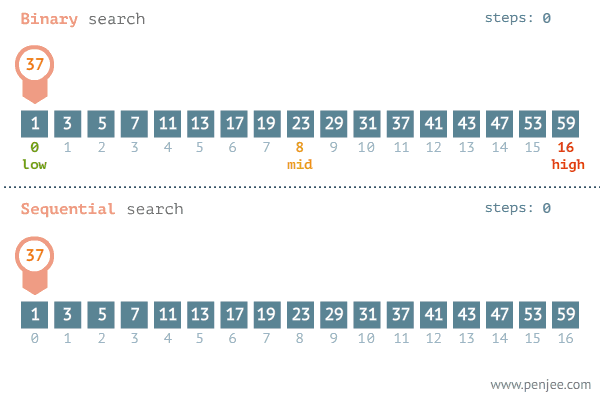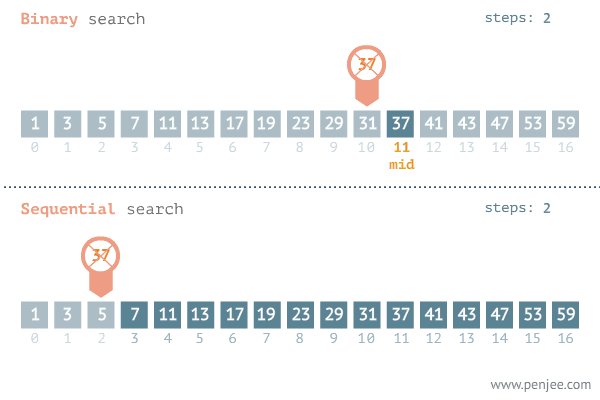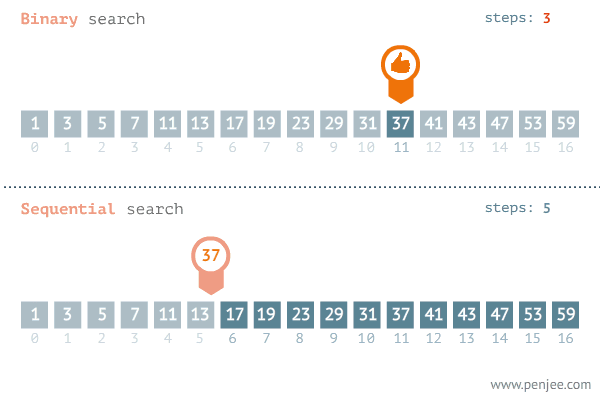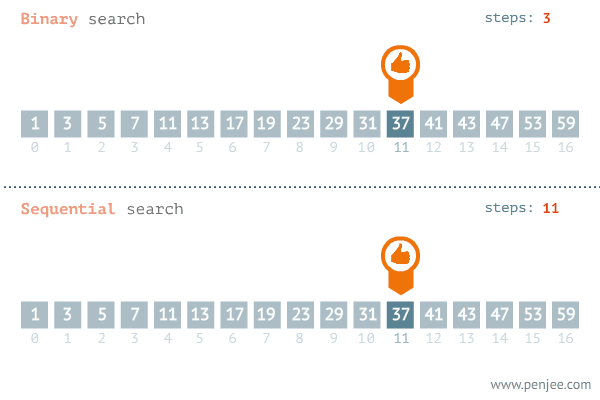
let binaryInteractive = (arr, x) => {
  let start = 0;
  let end = arr.length - 1;
  while (start <= end) {
    let mid = Math.floor((start + end) / 2);
    let target = arr[mid];
    if (target === x) {
      return mid;
    } else if (target > x) {
      end = mid - 1;
    } else {
      start = mid + 1;
    }
  }
  return -1;
};

Or we could

let binaryRecursive = (arr, ele, start, end) => {
  let mid = Math.floor((start + end) / 2);
  if (ele === arr[mid]) return mid;
  else if (ele > arr[mid]) {
    return binaryRecursive(arr, ele, mid + 1, end);
  } else {
    return binaryRecursive(arr, ele, start, mid - 1);
  }
};

# Backtracking Algorithms

Have you ever encounter a situation while coding, let’s say solving a problem and then you realized you made a mistake and you have to Ctrl-z back all the way where you think the mistake happened and you start thinking for alternative way until you gets the solution of the problem. That’s what backtracking basically is .

It is an algorithmic technique for solving problems recursively trying one solution after another and removing the solutions that failed the expected outcome of the algorithm.

Backtracking algorithms are use in scenarios where the solution is the sequence of choices and where making a choices impact or restrains sub-sequenct choices. So when you face the situation where the choice you made cannot give the solution you want so you step back and try something else.

Famous Eight Queens Puzzel 👑 How do you place eight queens on a chess board without each queens attack each other ?

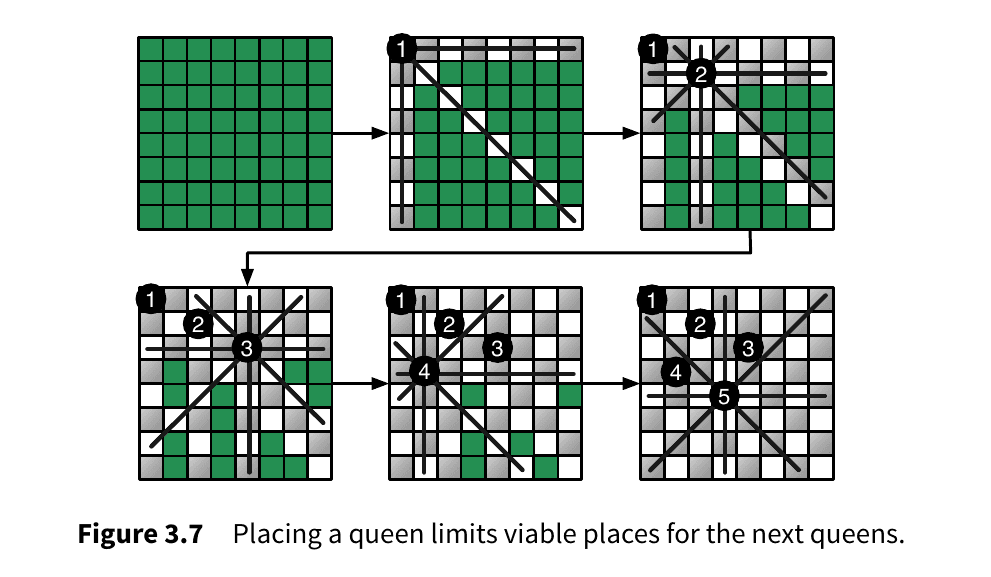
# Greedy algorithms

As the name suggests the greedy algorithm means greedily choosing the best available solution and always choosing the best next pieces that get the immediate effect.

For a simple analogy, when you go to your go-to bar on a Friday night with your friends and then the waiter told you that you will have to wait for about 40 minutes for your favorite drink as they run out of stock or whatever. And then you order your second favorite and talk and talk. After 40 min when your favorite drink is ready, you realized there is a pile of bottles of your second favorite brand on the table. You are drunk already to taste your favorite Friday gem. You may probably take it but you cannot tell the difference anymore.

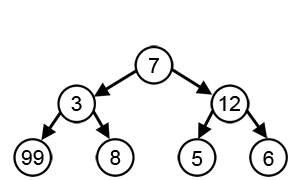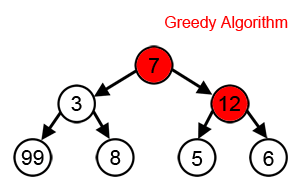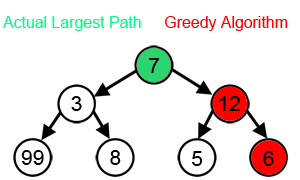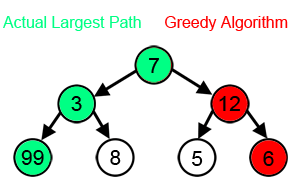
In the image below while finding the longest path, the greedy algorithm will always choose what seems optimal based on information at one step. Starting from 7 then 12 and 6. However, as you can see the algorithm does not give the correct answer. By greedily choosing the best locals, it is likely to skip the optimal for the overall problem.
Courtesy : brilliant.org

But when it works, the greedy algorithm gives us the perfect solution. For example, imagine you are a famous actor and you will have to schedule your timetable to get maximum movies contract for the year without two events overlapping (starting months or ending months of one movie do not fall between the starting and ending points of another movie). Let's say you have seven movies with different month periods.

How will you schedule your movies in order?

By greedy algorithm, we choose B, E, and C, and choose our movies by their ending time which we get the maximum movie that we can have in the year.

# Dynamic Programming Algorithms

Another type of algorithm that is commonly used is the dynamic programming algorithm. To talk about this kind of algorithm let's take a step back and look at how we did the Fibonacci algorithm using recursive. For convenience

function factorial(n) {
  if (n == 0) return 1;
  return n * factorial(n - 1);
}

As you can see in the above code, the recursive algorithm find out the Fibonacci in this structure

Courtasy : educative.io

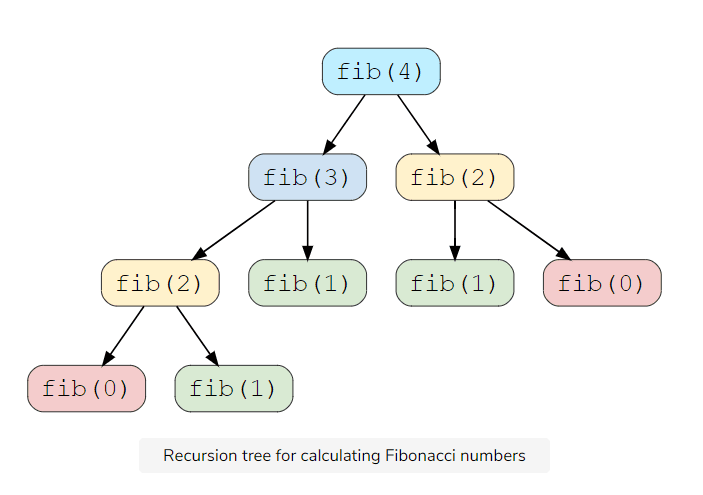
As you can see in the tree, it calculates the fab(4) into pieces by pieces and there is some overlapping function that gets called multiple times such as fib(2) two times and fib(1) three times. As great as a recursive function can be, a recursive program usually has a greater space requirement compared to an interactive program as it will remain in the execution stack until the base case is resolved. Dynamic programming is mainly an optimization over a recursive algorithm. When we see a recursive solution that gets called repeatedly on some input, we somehow memorize the result of the subproblem and we won’t have to recalculate again for upcoming similar subproblems.

const calculateFibonacci = function (n) {
  const memoize = [];

  function fib(n) {
    if (n < 2) return n;

    // if we have already solved this subproblem, simply return the result from the cache
    if (memoize[n]) return memoize[n];

    memoize[n] = fib(n - 1) + fib(n - 2);
    return memoize[n];
  }

  return fib(n);
};

# Hashing algorithms

There are also multiple types of hashing algorithms.As the internet grows, we got more and more data to be stored, accessed and search. We got arrays to store multiple type of data in a various way but in terms of efficiency arrays data structures take O(1) time complexity to be stored and accessed but in searching it takes at least O(logn) times.

So we use data structures like hash data structure to be store or retrieve data in constant time. With the help of a key to determine the index or location of a item in a data structure, the hash function recieve the input key and then find and give back the value or element from the hash table which essentially maps the keys to the values.

# Algorithms in the ideal world?

Even in the ideal world where your computer is indefinitely fast and the memory never runs out in your computer. You will still be using algorithms to demonstrate how your solution performs or terminate or if the algorithm gives you the perfect solution in the most effective way. If computers are indefinitely fast, maybe any approach to solving a problem could do the job. However, you will still be making sure that your algorithm is implemented with great engineering practice or that your implementation is very well designed and well documented. Of course with the easiest method to implement.

# Efficiency

We are not still in the ideal world so we will still be trying to maximize our algorithm’s efficiency in the best possible way. Let’s say we compare two algorithms one with the big O of $O(n^2)$ and the other with $O(logn)$ . Also, let’s pick two computers to run those programs in parallel in the name of science to compare how they perform. We have one very fast computer and one very slow one and they both will have to solve an array of 10 million numbers. We use two sorting algorithms insertion sort $O(n^2)$ and merge sort $O(logn)$ . Suppose the fast computer executes 10 billion executions per second and the slow one only 10 million per second. So the fast one is 1000 times faster than the slow one.

We have $n = 10^7$

We gonna run the insertion sort on the fast one and it runs approximately,

And the slow one with merge sort takes

(10^7)^2 instructions / (10)^{10} instruction.p.sec \approx 10,000 seconds

10^7 lg 10^7 instructions / 10^7 execution.p.sec \approx 7 seconds

The larger the data size is the better we can see the performance difference in both algorithms.

Courtesy : Computer Science Distilled

# Analysis of algorithms

While analyzing an algorithm, occasionally our algorithm might depend on physical resources such as memory, communication, and computer hardware. Since analyzing it means we need to predict the resources that an algorithm might require. But instead of measuring the actual running time of an algorithm which is impossible, we measure the running time of the algorithm by counting the number of steps of execution that an algorithm takes on a given input.

One of the popular machine models is called RAM ( Random Access Machine ). In the hypothetical RAM machine, without running the algorithms on an actual physical machine we consider steps by,

Simple operations such as (+,-*,/,- ) take one step
loops and other sub-operations are composed of simple operations and
memory is unlimited

RAM works very well in counting how many steps an algorithm might take to solve a certain problem. We measure for a certain input of n

The best case complexity is the minimum of steps it takes for an algorithm to complete. For example, linear search in an array where the target element is the first element.
The worst case complexity is where the linear search in an array where the target element does not exists or is the last element.
The average case where the element is in the center so to speak.

In the real world, the worst case complexity is the most useful measurement because it is unlikely for the input of an algorithm to be best case oriented. For reliable algorithms, we should prepare for the worst and it is easy to calculate.

What are time and space complexities ?

Refs