Merge Sort: A Divide-and-Conquer Sorting Algorithm

When I first learned about sorting algorithms, I was really impressed by how merge sort works. I feel smart while writing it. By breaking down a large array into smaller, more manageable subarrays and then merging them back together in sorted order, merge sort allows for efficient and effective sorting of large amounts of data.

Merge sort is a great way to sort big sets of data because it works well and is simple to use. People often use it alongside other algorithms, such as quicksort (which I will explain later in my blog), to make the sorting process even more efficient.

# How does merge sort work?

Let's think of this process as breaking down the array into smaller and smaller parts until it can no longer be broken down. This is called the base case, which occurs when the array is empty or has only one element remaining.

If the array has more than one element, it is split into halves and the process is repeated on each half. Once both halves are sorted, they are combined to create a larger sorted array. This final step is called the merge operation.

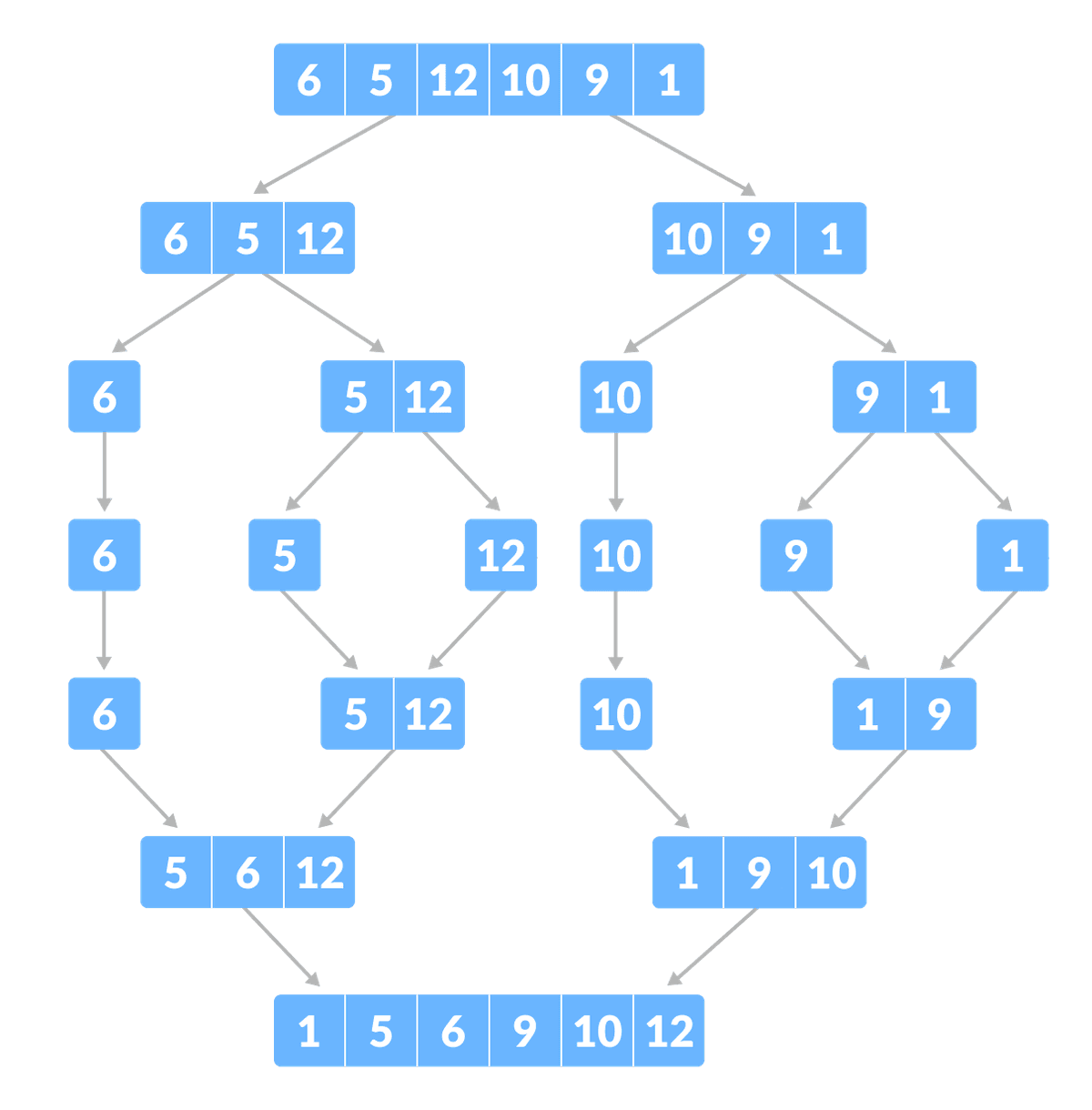
# Divide and conquer strategy

By using the Divide and Conquer technique, we can break down a problem into smaller subproblems. Once we have solved each subproblem, we can then combine the results to solve the main problem.

Let's say we have the following array of numbers:

[5, 1, 9, 3, 7, 6, 4, 8, 2]

First, we need to divide it into two halves:

[5, 1, 9, 3, 7] and [6, 4, 8, 2]

Then, we need to divide each of these halves into two more halves:

[5, 1, 9] and [3, 7], [6, 4, 8] and [2]

We continue dividing each subarray until we reach the base case, where we have subarrays with only one element:

[5], [1], [9], [3], [7], [6], [4], [8], [2]

Next, we start merging the subarrays, two at a time, in sorted order. For example, we first merge [5] and [1] to get [1, 5], then merge [9] and [3] to get [3, 9], and so on.

We continue merging pairs of subarrays until we have one large sorted array:

[1, 5, 3, 9, 7, 6, 4, 8, 2]

Finally, we merge the last two subarrays to get the fully sorted array:

[1, 2, 3, 4, 5, 6, 7, 8, 9]

# Time and Space Complexity of merge sort

Merge sort has a big advantage: it always runs quickly, with a consistent and guaranteed run time in the order of $O(n log(n))$. This means that no matter how the input data is structured, the algorithm will always work at this speed.

Merge sort has several advantages over other sorting algorithms. Not only does it have a worst-case time complexity of $O(n log n)$, which makes it efficient for large data sets, but it is also a stable sorting algorithm. This means that if there are two elements in the input array that are equal, their relative order will be preserved in the output array. Having stability is crucial for specific applications where the order of equal elements must be preserved.

For example, in a list of names, if two people have the same name, it might be important to preserve the order in which they appear in the original list.This is in contrast to other sorting algorithms, such as quicksort, which are not stable.

Also, the merge sort algorithm splits the sorting process into smaller sub-problems that can be solved recursively.

Merge sort is known to use a lot of memory due to the need to store the subarrays during the sorting process. This can be a disadvantage when working with very large datasets.

function merge(left: number[], right: number[]) {
  let result = [];
  while (left.length && right.length) {
    if (left[0] < right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }
  return result.concat(left, right);
}
export function merge_sort(arr: number[]) {
  if (arr.length < 2) return arr;
  let length = arr.length;
  let mid = Math.floor(length / 2);
  let leftArr = arr.slice(0, mid);
  let rightArr = arr.slice(mid);
  let sortedLeft = merge_sort(leftArr);
  let sortedRight = merge_sort(rightArr);
  return merge(sortedLeft, sortedRight);
}